AHC022の配置時コストの最小化¶

概要¶

AHC022の配置時コストが最小になるような各セルでの温度設定について。

背景¶

配置の仕方として、基本は低い温度で、何点か高い温度の地点を用意して、そこを狙って観測することで位置を特定したい
ただ、1つのセルを高い温度(1000)にして、その周囲4セルが低い温度(0)にするなどすると、配置時コストが大きくなってしまうため、固定セル以外はコストができるだけ小さくなるように設定したい
コスト関数を微分して各地点での勾配を求めると、勾配降下法などで最適化できる
- 他のアプローチもあるが、ここでは、勾配降下法でのアプローチで試す

コストの最小化¶

参考: https://qiita.com/jkdorayaki/items/3f7d581b70c7881c7a5f
各セルの値が変数P(y,x)として、コストを最小化したいので、勾配(微分)を求めて、勾配降下法を適用する
- 勾配は、コストをP(y,x)で偏微分すると、セルの値から周囲4セルの平均値を引いた形になる
勾配降下法を適用すると、学習率η=1 / 8に設定した場合、周囲の平均に置き換えるような更新になる
- $P(y,x)' = P(y,x) - η \frac{\partial{cost}}{\partial{P(y,x)}}$
- $P(y,x)' = P(y,x) - η * 8 * (P(y,x) - 周囲の平均)$
- $P(y,x)' = (1 - η * 8) * P(y,x) + η * 8 * 周囲の平均$
- 学習率η = 1 / 8とすると、
- $P(y,x)' = 周囲の平均$

例¶

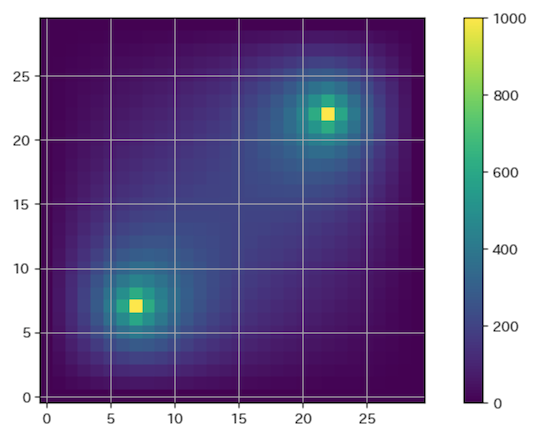
角の4辺を0、2箇所を1000としたとき、配置コストが最小になるようにその周囲を調整した場合。

#include <iomanip>
#include <iostream>
#include <vector>

constexpr int vy[4] = {-1, 0, 1, 0};
constexpr int vx[4] = {0, -1, 0, 1};

int main() {
    constexpr int L = 30;
    std::vector<std::vector<double>> p(L, std::vector<double>(L, 0));
    std::vector<std::vector<bool>> cnst(L, std::vector<bool>(L, false));

    //
    auto set_cnst = [&](int y, int x, double c) {
        cnst[y][x] = true;
        p[y][x] = c;
    };
    for (int i = 0; i < L; i++) {
        set_cnst(0, i, 0);
        set_cnst(L - 1, i, 0);
        set_cnst(i, 0, 0);
        set_cnst(i, L - 1, 0);
    }
    set_cnst(L / 4, L / 4, 1000);
    set_cnst(L * 3 / 4, L * 3 / 4, 1000);

    //
    for (int t = 0; t < 10000; t++) {
        auto np = p;

        for (int y = 0; y < L; y++) {
            for (int x = 0; x < L; x++) {
                if (cnst[y][x]) continue;

                // 周囲の値の平均値
                double ave = 0;
                for (int k = 0; k < 4; k++) {
                    const int ny = (y + vy[k] + L) % L;
                    const int nx = (x + vx[k] + L) % L;
                    ave += p[ny][nx];
                }
                ave /= 4;

                np[y][x] = ave;
            }
        }

        swap(p, np);
    }

    for (int y = 0; y < L; y++) {
        for (int x = 0; x < L; x++) {
            std::cout << (int)p[y][x] << "\t";
        }
        std::cout << std::endl;
    }

    return 0;
}

data = []
with open("out.txt") as f:
    for line in f:
        sp = list(map(int, line.rstrip().split("\t")))
        data.append(sp)

fig, ax = plt.subplots()
im = ax.imshow(data, origin="lower")
plt.colorbar(im)
plt.show()

	配置時コスト
2地点だけ1000に設定	8000000
2地点からBFSで-200ずつ小さく配置	8000000
2地点からBFSで0.35倍ずつ小さく配置	4927112
勾配降下法	3161528

変分原理¶

配置時コストは、Poisson方程式などの変分原理でのものと(ほぼ)同じ形になっている
- 微分方程式の問題を極値問題に帰着させることを変分原理というらしい
- 以下の汎関数
- $J(\phi) = \int( (\frac{\partial^2 \phi}{\partial x^2})^2 + (\frac{\partial^2 \phi}{\partial y^2})^2 - 2f\phi )dxdy$
- に変分法を適用すると、Poisson方程式 $\nabla^2\phi = f(x,y)$ が得られる
- 離散化すると、勾配部分が次の格子点との差分の2乗で近似できるので、配置時コストと同じものが現れる
汎関数 $J(\phi)$ を最小化する問題として解ける