Skip to content

京セラプログラミングコンテスト(AtCoder Heuristic Contest 006)

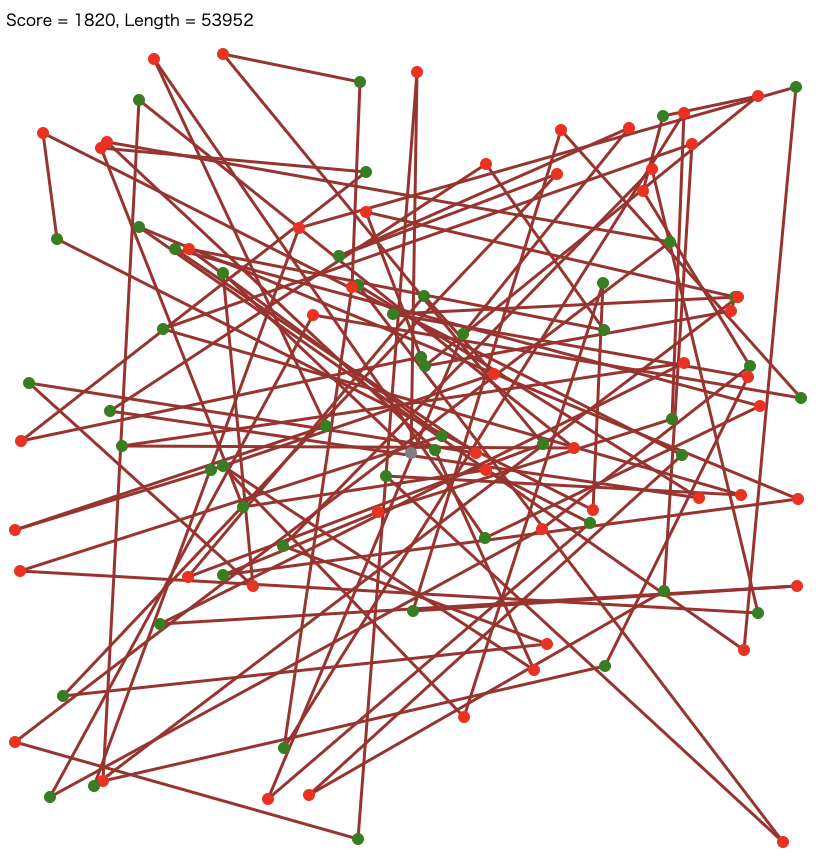
問題概要

  • 1000 個の配達の注文があり、各注文は二次元平面(0<=x,y<=800)上の地点 X のレストランから地点 Y への配達依頼になっている
    • レストランに着くと料理を受け取り、配達地点に着くと持っている料理の中から該当する料理を配達する
    • 料理はいくつでも受け取って持っておくことができる
    • 地点間の移動時間はマンハッタン距離で、総移動時間は地点間の時間の合計
    • 最初は(400,400)の地点からスタートし、最後も(400,400)の地点に戻ってくるようにする
  • このうち、50 個の注文を選び、総移動時間ができるだけ小さくなるような各地点の訪問順を求めよ

時間

240 分

個人的メモ

  • 見た目が TSP で、50 個をどう選ぶかと依存関係をどうするか
  • どちらも一緒に探索して、近傍として注文入れ替え時に最適位置に挿入するまでした場合が強かった模様
  • 差分更新したほうが良さそうに見えるが、バグ散らかしてしまった
    • 高速化が本当に必要かどうかもわからないうちから複雑な実装をすべきではない、、、

近傍

  • 2-opt
    • 依存関係があるので有効か？と思われるが、依存関係が壊れない範囲で適用可能
    • また、最終的な形として、結構レストランが連続していたり、配達地点が連続している解があるため、結構いい感じに発動できる模様
  • 注文を削除して、別の注文に置き換え。このとき、最適位置に挿入、が重要

その他

  • 貪欲解
  • 注文を挿入するビーム
  • レストラン/配達先を独立に計算(依存がなくなる)してくっつける
  • 偏角ソートして円の形で選出

解説

(50 位まで&発言を見つけられた方のみ)