Skip to content

トヨタ自動車プログラミングコンテスト2024#10(AHC038)

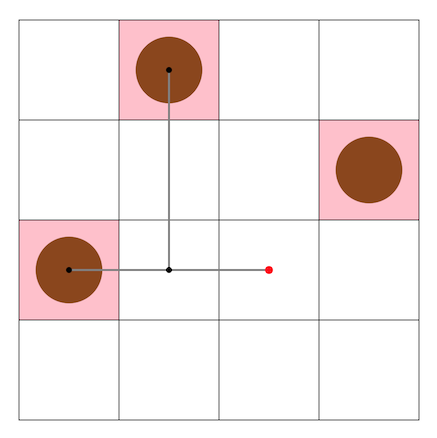
問題概要

  • N * Nマスのたこ焼き器があり、Mマスにたこ焼きが置かれており、これを指定されたMマスの目的地に移動させたい
  • 移動には、あらかじめ設計した木構造のロボットアームを使うことができ、葉の指すマスに対してたこ焼きを掴む、置く操作が行える
    • ロボットアームは、V頂点からなる木構造で、軸に並行に配置され、毎ターン、根位置の移動、90度回転、たこ焼き操作が行える
  • ロボットアームの設計を行い、できるだけ少ないターンで目的地に移動する操作列を求めよ

時間

  • 240 時間

個人的メモ

ロボットアーム設計

根のみ

  • 1番単純なのは、1頂点(根のみ)で運ぶケース
  • 運ぶのに1ターンで1マスしか動けないため、移動分だけターンが必要になってしまう

スター型

  • 「根のみ」の拡張として、根から辺をたくさん生やすことで、(だいたい)同時に運べるようになる
    • この場合は、AHC006的な感じ？
  • 同時に運べるためターンは減るが、根のみの場合と同様に、移動分のターンが多く必要

パス型

  • 長い辺を考えた場合、90度回転させることでかなりの長距離を1ターンで移動することができる
    • 長さがLの辺のみのアーム(●--------oみたいなの)で考えると、90度回転した位置へは、根の移動のみで動かすと2Lターンかかるところが、回転操作の1ターンでできる
  • また、直線的につなげた辺つなげた●--------o-------o----oのような形を考えると、1ターンで移動できる位置が増加する
  • それぞれの長さが「16,8,4,2,1」のものを考えると、すべてのNで、中心からすべての位置に2ターン以下でアクセスできるので、「少なくとも2ターン*移動が必要なたこ焼き数」を達成できる

箒型(パス＋スター)

               o
               |
●------o----o--o----o
               |\
               | \
               o  \
                   o
  • 上記のような、パスの先端や途中の頂点からスター型のように辺を生やすと、長距離移動＆同時移動が両立できる
  • 最終的には、1ターンで大量に拾って1ターンで大量に置く、を繰り返す感じにしたいため、同じ長さのスターではなく、長さを1,2,3,4,...のように分けて同時に操作できるようにするなどが考えられる
  • パス側に頂点を使うか？スター部分に頂点を使うか？
    • パス部分の頂点を1頂点減らすと、移動できる範囲が減ってしまうが、代わりに並列数が1増える
  • バリエーション
    • 頂点数、生やし方、辺の長さなどの工夫が可能
    • V=5やVが大きい場合は、うまく形状を変えると、より良くなる可能性がある

パス部分の長さ(「8,4,2,1」型/「1,2,4,8」型)

V=5の場合

  • 5頂点しか使えない場合、頂点数に余裕がないため、8-4-2-1のように構成すると、1つずつしかたこ焼きが移動できない
  • うまくパス部分の頂点を減らして、スター部分に頂点を使えないか探せると、スコアが大きく変わりうる
    • Nが小さかったり、葉の数を増やせるケースの場合は、2〜3個同時に移動できるため、並列化効果がかなり大きい

アームの探索、埋め込み

  • NやVによって必要な長さや葉の個数が変わったり、各ケースのたこ焼きの数(M)や配置によって、変わりうる
  • アームの形状は「決め打ち」するか「ケースに合わせて探索」するかが考えられるが、今回は、どちらでも上位を目指せた模様
    • NやVで固定で埋め込む
    • 貪欲などで試してみて一番良かったやつを採用して、より時間をかけて探索する

操作列の探索

  • アームの形状が決まったら、最短手数で移動できる操作列を探索する
  • 上位は、ビームサーチ/chokudaiサーチか、貪欲が多かった模様

次の状態の生成

  • ある状態に対して、次の状態を考える場合、1手で動かせるのは、「ルートの位置5通り＋アームの状態3V＋拾うか置くか2{葉の個数}」だけありえてしまう
  • 箒型のアームの場合、ルートの位置とパス部分のアームの状態だけ全探索し、葉の向きや拾うか置くかは貪欲に決めるように考えると、かなり無駄な状態を減らせる
  • 「1回休み」
    • 直前で何もしない葉は、180度(2ターン分)操作可能
    • パス部分も、1個もたこ焼きを取れない場合、1回休みとすると、根の距離と状態の差だけ見れば遷移可能かがわかり、無駄に状態を増やさなくて済む
  • 次にどこにも拾う/置くができない場合、「1回休み」になるが、その近くに拾う/置くができる場所がなければある程度の移動が必要なため、そのような場合は、できる位置まで大きく移動させる
    • そのような位置は別途探索する

評価関数

  • 拾った・置いたたこ焼き数
    • 2*M個の進捗として考える
  • たこ焼きの重要度(取れる状態数、外側にあるか、など)
  • 1列消しに対して加点

その他

操作回数の理論値

  • 理論値的には、拾う&置くがそれぞれ1ターンで行えた場合、「移動が必要なたこ焼き数 / 同時に移動できるたこ焼き数 * 2(拾う&置く分)」になる
    • この時、回答の後ろの部分はPで埋まっている感じになる
    • ケースによってスコアが結構バラけるので、上記で正規化するとよいかも
    • ただし、「同時に移動できるたこ焼き数」はアーム設計依存

中継

  • 「ある地点を経由して移動する」というのも考えられる
  • ただ、今回は考慮しなくても良かった模様

厳しいケース

  • seed=5333(N=30,M=266,V=5)

お絵かき

解説

(50位まで&発言を見つけられた方のみ)